Introducción
Las figuras geométricas juegan un papel crucial en el entendimiento del mundo que nos rodea, ofreciendo herramientas para describir y analizar fenómenos físicos y matemáticos.
En este artículo, exploraremos las 10 principales diferencias entre parábola e hipérbola, dos de las secciones cónicas que, aunque derivan de cortes de un cono a diferentes ángulos, presentan propiedades y aplicaciones distintas. Su estudio no solo es fundamental para las matemáticas sino también para diversas aplicaciones en física, ingeniería y otras ciencias.
Diferencias
-
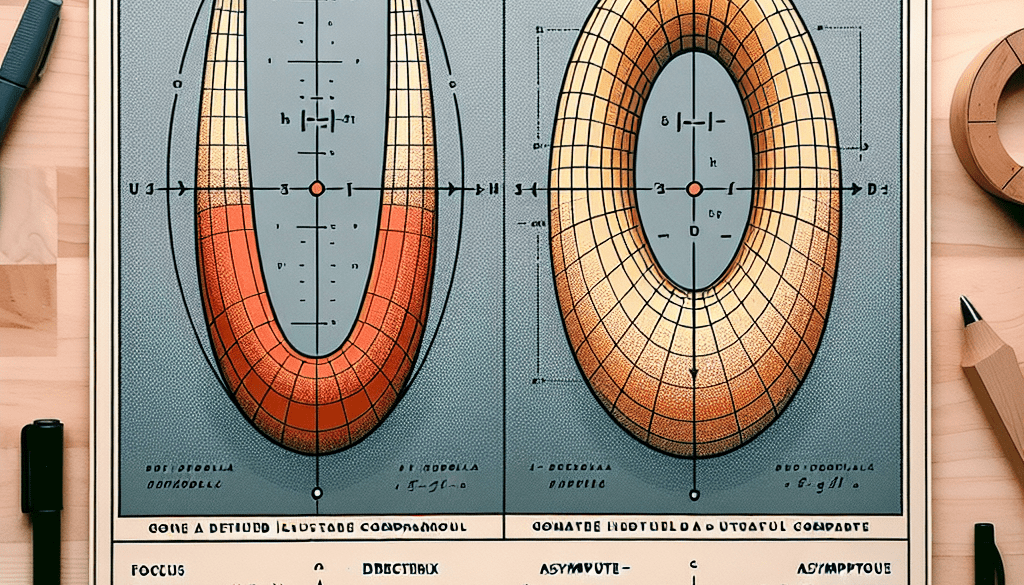
Definición geométrica: Una parábola es el conjunto de todos los puntos equidistantes de un punto fijo llamado foco y una línea fija llamada directriz. Una hipérbola se compone de dos ramas separadas, cada una formada por los puntos cuya diferencia de distancias a dos puntos fijos, llamados focos, es constante.
-
Ecuaciones estándar: La forma más común de representar matemáticamente una parábola implica una ecuación donde una variable se eleva al cuadrado y se iguala a una constante multiplicada por la otra variable. Por otro lado, la ecuación estándar de una hipérbola implica la diferencia entre los cuadrados de las variables, cada uno dividido por una constante, y esta diferencia se iguala a uno. Esto refleja la naturaleza simétrica pero divergente de las hipérbolas en comparación con la estructura más focalizada de las parábolas.
-
Dirección de apertura: Las parábolas se abren hacia arriba o hacia abajo (en el caso de las funciones cuadráticas) o hacia la izquierda o derecha (en el caso de parábolas horizontales). Las hipérbolas se abren hacia dos direcciones opuestas, formando dos ramas separadas que se extienden hasta el infinito.
-
Asíntotas: Las parábolas no tienen asíntotas, ya que se extienden indefinidamente en una sola dirección sin aproximarse a una línea recta. Las hipérbolas tienen dos asíntotas que son líneas rectas intersectándose en el centro de la hipérbola, ofreciendo un límite visual hacia el cual las ramas de la hipérbola se extienden infinitamente.
-
Aplicaciones: Las parábolas tienen aplicaciones en óptica y mecánica, como reflejar la luz y el sonido hacia un foco. Las hipérbolas aparecen en la navegación y astronomía, por ejemplo, en la determinación de órbitas de objetos que escapan de la atracción gravitacional de un cuerpo celeste.
-
Propiedades de reflexión: Las parábolas tienen la propiedad única de que los rayos paralelos al eje principal se reflejan en el foco. Las hipérbolas no comparten esta propiedad debido a su estructura abierta en dos ramas.
-
Focos y directrices: Tanto parábolas como hipérbolas tienen focos y directrices, pero en la parábola, hay un solo foco y una directriz, mientras que en la hipérbola, hay dos focos y dos directrices, cada una asociada con una rama de la hipérbola.
-
Eje de simetría: La parábola tiene un único eje de simetría que pasa por su foco y vértice. La hipérbola tiene dos ejes de simetría: uno pasa por los dos focos, y el otro es perpendicular al primero y pasa por el centro de la hipérbola.
-
Centro: El centro de una parábola se considera en el vértice, el punto medio de la parábola. En contraste, el centro de una hipérbola es el punto medio entre sus dos focos, desde donde se dibujan las asíntotas.
-
Naturaleza de las curvas: La parábola es una curva simple que se extiende en una dirección. La hipérbola es una curva doble que se extiende en dos direcciones opuestas, formando dos ramas separadas.
Conclusión
Comprender las diferencias entre parábolas e hipérbolas nos permite apreciar la diversidad y la belleza de las formas geométricas en el mundo que nos rodea. Estas dos curvas, fundamentales en el estudio de las secciones cónicas, tienen propiedades y aplicaciones únicas que se extienden más allá de la teoría matemática, influyendo en campos tan variados como la física, la ingeniería y el arte.
A través de este análisis, hemos visto cómo la parábola y la hipérbola sirven como ejemplos poderosos de cómo los principios matemáticos se manifiestan en el mundo natural y construido, demostrando que incluso las diferencias sutiles en las ecuaciones pueden dar lugar a formas con características y funciones profundamente distintas. Este conocimiento no solo enriquece nuestra comprensión de las matemáticas, sino que también fomenta una apreciación más profunda de la complejidad y elegancia inherentes al universo.

