Introducción
En geometría, el círculo y la elipse son dos formas básicas que a menudo se confunden debido a sus similitudes.
En este artículo, exploraremos las 10 principales diferencias entre círculo y elipse.
Mientras que el círculo es una figura geométrica perfectamente redonda con todos los puntos equidistantes de su centro, la elipse es una forma ovalada con dos puntos focales.
¡Vamos a descubrir qué las hace únicas y cómo se diferencian!
Diferencias
- Definición: Un círculo es una figura geométrica plana en la que todos los puntos están a una distancia constante (radio) de un punto fijo (centro). Una elipse es una figura geométrica plana en la que la suma de las distancias desde cualquier punto de la elipse a dos puntos fijos (focos) es constante.
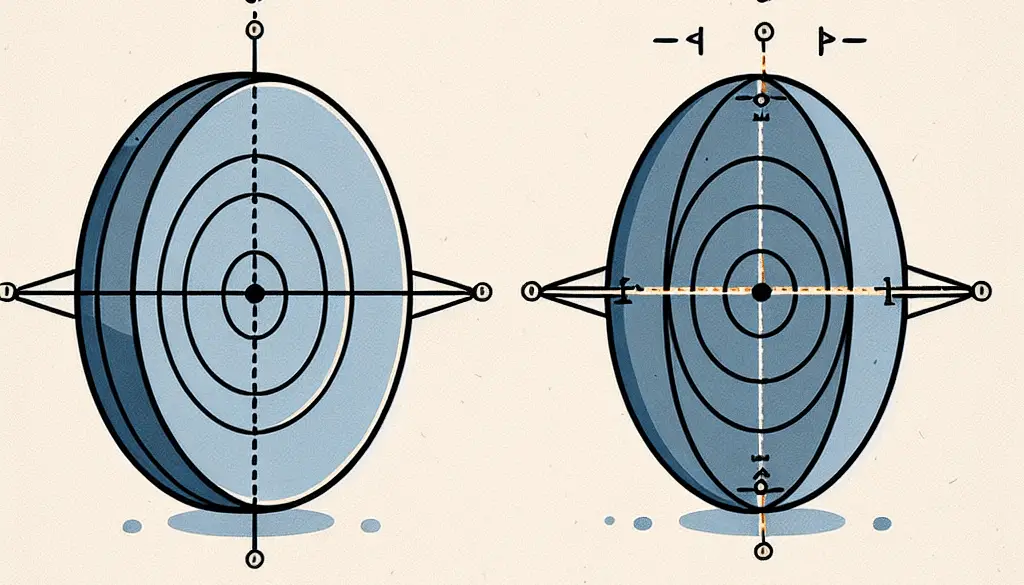
- Centro y Focos: El círculo tiene un solo punto central y todos los puntos del círculo están equidistantes de este centro. La elipse tiene dos focos y la distancia total desde cualquier punto de la elipse a estos dos focos es siempre la misma.
- Ecuación matemática: La ecuación estándar de un círculo en el plano cartesiano es (x – h)² + (y – k)² = r², donde (h, k) es el centro y r es el radio. La ecuación estándar de una elipse con los ejes alineados con los ejes coordenados es (x – h)²/a² + (y – k)²/b² = 1, donde (h, k) es el centro y a y b son las longitudes de los semiejes mayor y menor, respectivamente.
- Radios: En un círculo, el radio es constante en todas las direcciones desde el centro. En una elipse, hay dos radios principales: el semieje mayor (a), que es la distancia más larga desde el centro hasta el borde, y el semieje menor (b), que es la distancia más corta desde el centro hasta el borde.
- Simetría: Un círculo es perfectamente simétrico en todas las direcciones y tiene una simetría infinita de rotación. Una elipse tiene simetría bilateral a lo largo de sus dos ejes principales, pero no tiene la misma simetría de rotación que un círculo.
- Forma y apariencia: Un círculo siempre tiene una forma perfectamente redonda. Una elipse tiene una forma ovalada, alargada en la dirección del semieje mayor y más estrecha en la dirección del semieje menor.
- Curvatura: La curvatura de un círculo es constante en todos sus puntos. La curvatura de una elipse varía a lo largo de su borde, siendo mayor en los extremos del semieje menor y menor en los extremos del semieje mayor.
- Área: El área de un círculo se calcula con la fórmula A = πr², donde r es el radio. El área de una elipse se calcula con la fórmula A = πab, donde a es el semieje mayor y b es el semieje menor.
- Circunferencia y Perímetro: La circunferencia de un círculo se calcula con la fórmula C = 2πr. El perímetro de una elipse no tiene una fórmula simple como la del círculo, pero puede aproximarse con la fórmula P ≈ π[3(a + b) – √((3a + b)(a + 3b))].
- Aplicaciones prácticas: Los círculos se encuentran comúnmente en aplicaciones que requieren simetría perfecta, como ruedas, relojes y platos. Las elipses se encuentran en aplicaciones como órbitas planetarias, reflectores y diseño arquitectónico, donde las propiedades de la forma ovalada son útiles.
Conclusión
En resumen, aunque el círculo y la elipse son formas geométricas relacionadas, son distintas en términos de sus propiedades y aplicaciones.
El círculo es una figura perfectamente redonda con todos los puntos equidistantes de su centro, mientras que la elipse es una figura ovalada con dos focos y radios distintos. Comprender estas diferencias es crucial para aplicaciones en matemáticas, física, ingeniería y otras disciplinas.
Para finalizar, te presentamos una tabla de resumen de diferencias entre círculo y elipse:
| Aspecto | Círculo | Elipse |
|---|---|---|
| Definición | Todos los puntos a una distancia constante del centro | Suma de las distancias a dos focos es constante |
| Centro y Focos | Un solo centro | Dos focos |
| Ecuación matemática | (x – h)² + (y – k)² = r² | (x – h)²/a² + (y – k)²/b² = 1 |
| Radios | Un radio constante | Semieje mayor (a) y semieje menor (b) |
| Simetría | Simetría infinita de rotación | Simetría bilateral |
| Forma y apariencia | Perfectamente redonda | Ovalada |
| Curvatura | Constante | Varía a lo largo del borde |
| Área | A = πr² | A = πab |
| Circunferencia y Perímetro | C = 2πr | Aproximación: P ≈ π[3(a + b) – √((3a + b)(a + 3b))] |
| Aplicaciones prácticas | Ruedas, relojes, platos | Órbitas, reflectores, diseño arquitectónico |
Esta tabla resume las diferencias clave entre círculo y elipse, proporcionando una visión clara de cómo estas formas geométricas contribuyen a nuestras aplicaciones prácticas y comprensión del mundo.

